Кривая забывания Эббингауза в пользовательских приложениях

Привет, Tproger! Сегодня многие учат иностранные языки с помощью приложений - от популярных до простых Telegram-ботов. Но сталкивались ли вы с тем, что вроде бы выученное слово через пару дней вдруг исчезает из памяти? Спойлер: это не ваша проблема, а особенность человеческого мозга.

В этой статье я хочу познакомить вас с системой забывания, которую исследовал немецкий психолог Германн Эббингауз. Мы разберём, как перевести её в формулы, понятные программисту, как эту теорию я применил в своём Telegram-боте для изучения английских слов. Мы разберём практическую сторону, посмотрим на SQL-реализацию и наглядно сравним её с кодом на Python.

Кривая забывания Эббингауза

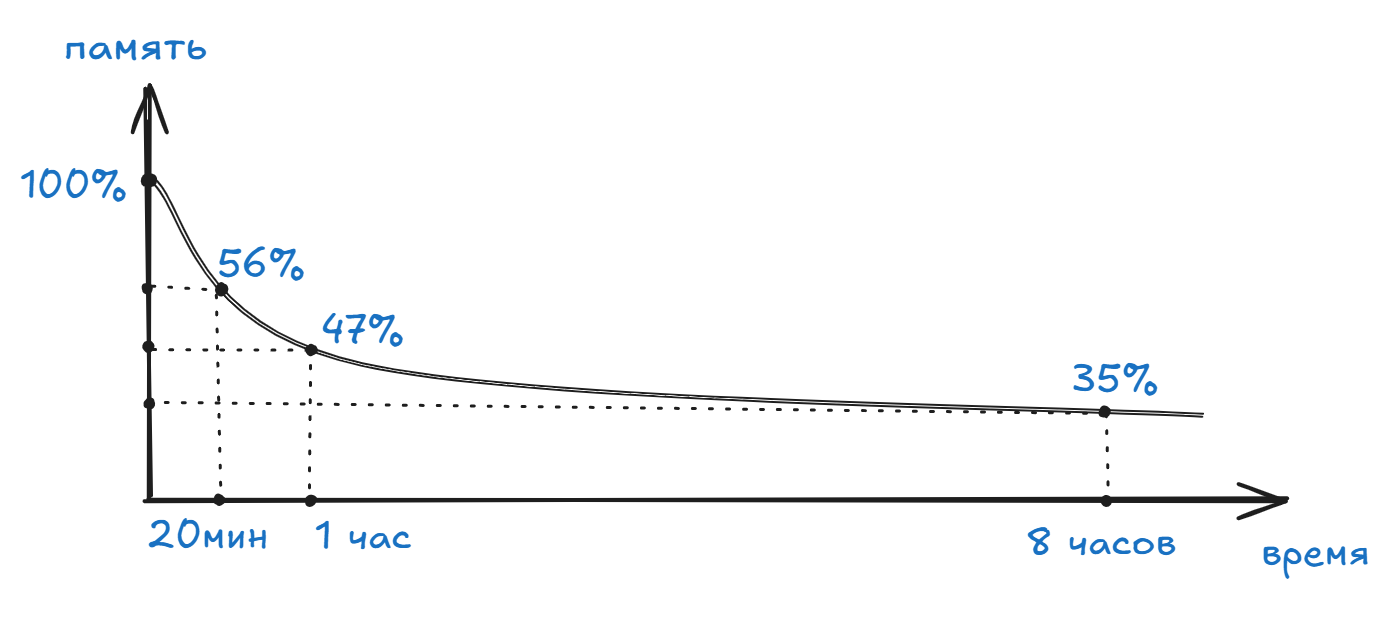
Суть теории проста, если выучить определённый объём несвязанных данных (в оригинальных экспериментах это были случайные слоги), то уже через 20 минут в памяти останется около 56%, через час - 47%, через 8 часов - 35%, и дальше спад идёт по экспоненте.

Эббингауз впервые экспериментально описал кривую забывания как зависимость сохранности материала от времени.

Кривая забывания Эббингауза

Согласно его фундаментальной работы "Memory: A Contribution to Experimental Psychology" формула выглядит так:

Формула забывания Эббингауза

Коэффициенты k и c были получены опытным путём, чтобы расчёты совпадали с реальными наблюдениями.

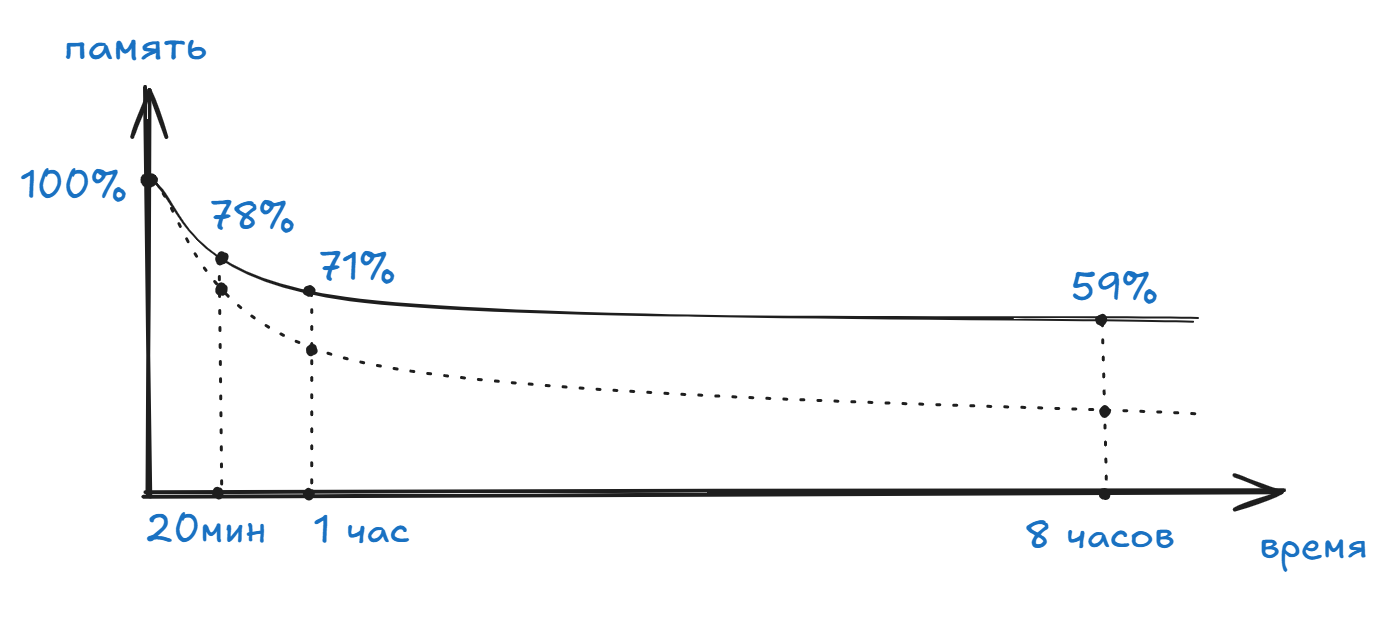
Давайте попробуем поиграть параметрами формулы и посмотреть как изменяется график. Если увеличить коэффициент k, кривая вытягивается вправо: всё забывается медленнее по всему диапазону. Вот график при коэффициенте k = 5. Пунктирной линией график с коэффициентом k = 1.84.

График при коэффициенте k = 5. Пунктирной линией график с коэффициентом k = 1.84.

C психологической точки зрения этот коэффициент можно трактовать как стабильность повторения ну или легкость элемента повторения.

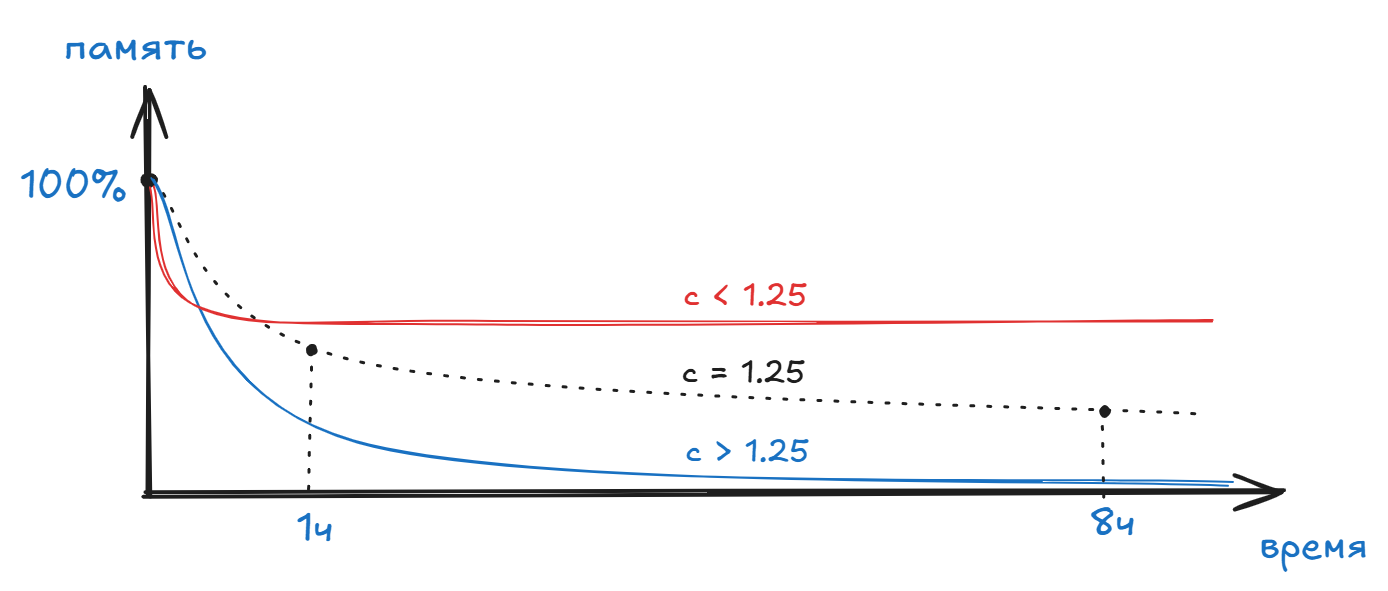
Коэффициент "с" - кривизна забывания. Он управляет тем, насколько быстро растёт вклад времени в знаменатель.

График при коэффициенте c < 1.25, c = 1.25, c > 1.25.

При c > 1.25 спад ускоряется сильнее, то есть весь изученный материал забывается раньше, а при c < 1.25 - резче падает сразу, но хвост длиннее (дольше «тянется» память на больших временах). Коэффициент будто «перераспределяет» забывание между ранней и поздней фазами.

Как перенести теорию в код

Теорию мы разобрали, теперь самое интересное применить её на практике. Представим, что у нас есть приложение для изучения английских слов. В моём случае это Telegram-бот, который ищет переводы, сохраняет их в «альбомы» и помогает учить через задания и тесты. Пользователь повторяет слова небольшими порциями, а приложение подсказывает, что стоит повторить прямо сейчас, а что можно оставить на потом.

И вот здесь мне понадобится кривая забывания. Алгоритм на её основе помогает автоматически решать: какое слово пора освежить в памяти, а какое можно отложить. Чем лучше ты справляешься с тестами, тем дольше приложение не будет тревожить тебя этим словом. Если же ошибок много, то слово будет попадаться чаще, пока не закрепится.

Если учесть, что коэффициент k поднимает и вытягивает кривую на графике, логично предположить, что при каждом правильном прохождении теста, этот коэффициент должен увеличиваться, а при неправильном снижаться. Назовем его коэффициент прочности, а описать его можно так:

			def coefficient_strength(correct_count, wrong_count):
  return max(correct_count * 0.8 - wrong_count * 0.5, 0)

		

Каждый правильный ответ (correct_count) повышает коэффициент прочности на 0.8, а каждый неправильный (wrong_count) снижает его на 0.5. Эти значения можно регулировать под конкретные задачи: сделать повторения чаще или реже, в зависимости от того, какой баланс между скоростью и качеством обучения вам нужен.

			def forgetting_curve(minutes, strength=0):
    memory_decay_factor = (math.log10(max(minutes, 1))) ** 1.25
    return 100 * (1.84 + strength) / (1.84 + strength + memory_decay_factor)
		

minutes - сколько прошло минут с момента повторения,

strength - коэффициент прочности, который мы описали выше.

max(minutes, 1) - используется, если между повторениями материала прошло меньше минуты, чтобы исключить отрицательно значение логарифма.

Для хранения параметров обучения в базе данных нам потребуется простая таблица words, которая состоит из 4 столбцов:

• text - само слово,
• last_review - время последнего повторения,
  
• correct_count и wrong_count - статистика ответов пользователя.
  

Если слов в обучении немного, мы можем просто выгрузить все данные из таблицы и выполнить расчёты прямо в приложении. Но по мере увеличения словаря такой подход становится неэффективным, потому что передача и обработка больших объёмов данных на стороне клиента сильно замедляет работу. Поэтому оптимальнее переносить вычисления на сторону базы данных. В этом случае сервер сразу возвращает только нужные слова, уже отсортированные по приоритету.

Например, в PostgreSQL это можно выразить напрямую в SQL-запросе:

			SELECT
    text,
    100 * (1.84 + GREATEST(correct_count * 0.8 - wrong_count * 0.5, 0))
        / (
            1.84 + GREATEST(correct_count * 0.8 - wrong_count * 0.5, 0)
            + POWER(LOG(GREATEST(EXTRACT(EPOCH FROM (NOW() - last_review)) / 60, 1)), 1.25)
        ) AS priority
FROM words
ORDER BY priority ASC
LIMIT 5;
		

priority - итоговый коэффициент по формуле Эббингауза, показывающий, какие слова стоит повторять в первую очередь.

Хочу поподробнее остановится на запросе и разобрать эту строчку:

			EXTRACT(EPOCH FROM (NOW() - last_review)) / 60
		

•  NOW() - возвращает текущее время базы данных (в PostgreSQL это timestamp with time zone),
• NOW() - last_review - разность двух времён, это объект типа interval
  
• EXTRACT(EPOCH FROM ...) - функция берёт определённое поле из даты или интервала,
  
• EPOCH - это количество секунд.

То есть EXTRACT(EPOCH FROM interval) преобразует интервал времени в число секунд, прошедших с момента последнего повторения.

Хочу обратить внимание на синтаксис функции логарифма в SQL и Python. В оригинальной формуле используется десятичный логарифм (common logarithm, основание 10). В PostgreSQL он записывается как LOG(x), тогда как в python math.log(x) или numpy.log(x) это натуральный логарифм по основанию e, а десятичный записывается как math.log10(x) или numpy.log10(x).

Визуализация забывания

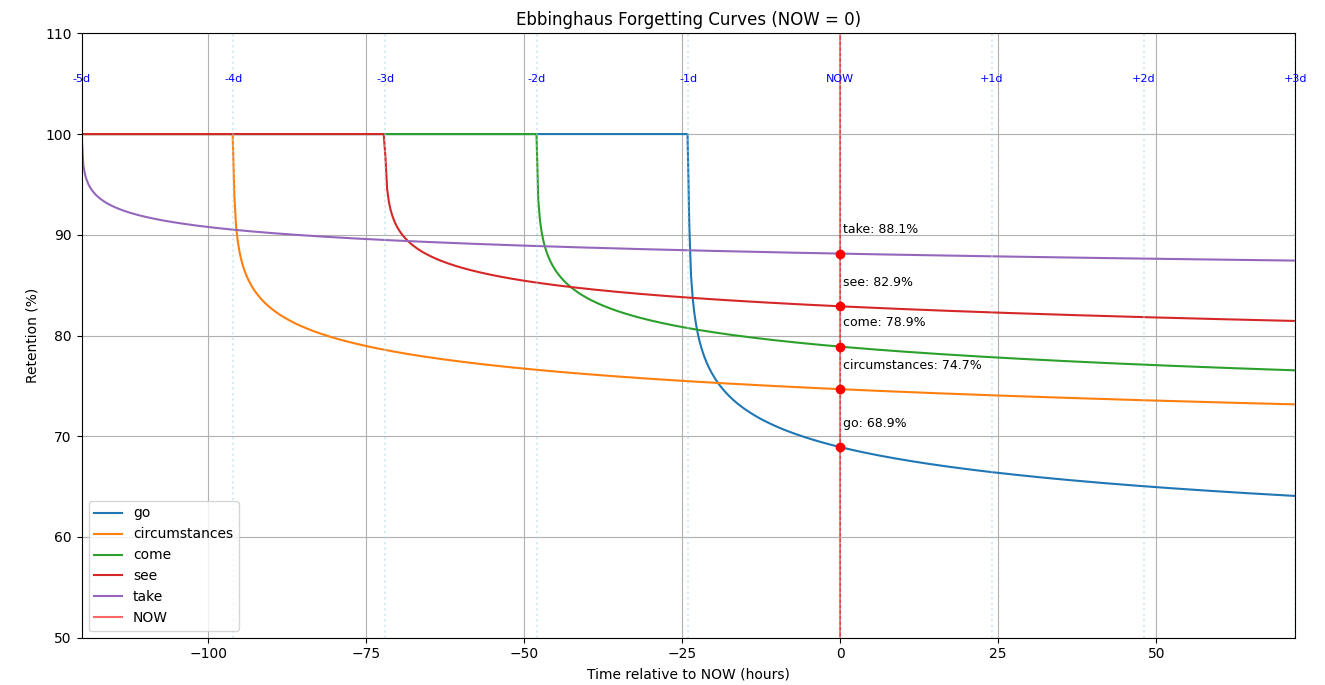
Для наглядности рассмотрим пять слов с разным временем последнего повторения и количеством правильных/неправильных ответов:

Таблица содержит пять слов с разным временем последнего повторения и количеством правильных/неправильных ответов.

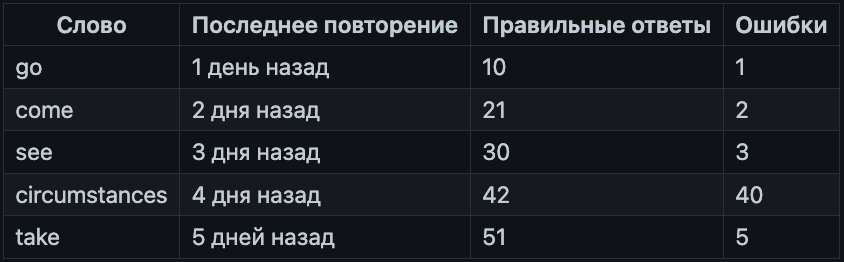
Эта таблица демонстрирует, что чем раньше мы начали учить слово, тем больше правильных ответов оно накапливает. Например, у take или see число успешных повторений значительно выше, чем у свежих слов go или come. В то же время слово circumstances выбивается из общей картины, хотя оно училось раньше других и должно было бы демонстрировать высокий уровень запоминания, большое количество ошибок (40 против 42 правильных) сильно снижает его «силу удержания» в памяти.

Построение кривых забывания для представленных слов

На графике хорошо заметно как кривая circumstances резко идёт вниз и оказывается ниже даже у более «молодых» слов. Этот пример наглядно показывает, что важен не только фактор времени последнего повторения, но и качество усвоения. Если слово систематически даётся с ошибками, его приоритет для повторения возрастает, и система будет предлагать его чаще.

Таким образом, сочетание параметров времени последнего повторения и статистики правильных/неправильных ответов позволяет адаптивно выстраивать план повторений. Это даёт более реалистичную модель памяти по сравнению с простой зависимостью только от времени, как у Эббингауза в классической формуле.

Подробный пример реализации с извлечением слов из базы данных по приоритету и построения графиков можно посмотреть в моём репозитории на GitHub.

Заключение

Формула Эббингауза - это лишь один из возможных подходов к решению задачи повторения, который я реализовал на SQL и Python. Очевидно, что в сети существуют более сложные и продвинутые решения, особенно с учётом развития машинного обучения и ИИ. Однако целью этой статьи было показать, как подобную модель можно реализовать просто без усложнения архитектуры. Коэффициенты и сама формула легко модифицируются. Их можно адаптировать под сложность материала, частоту ошибок или даже контекст использования знаний. Если у вас есть идеи, как улучшить модель или расширить её применение, буду рад обратной связи и обсуждению.